Available “heads” of Hydra
Hydra is a Gibbs sampler, which draws samples from the joint posterior distribution of the data model parameters by breaking it up into a set of conditional distributions and iterating through them. For each conditional distribution, samples are drawn from a subspace of the full parameter space while all other parameters are fixed (conditioned on). As the sampler iterates through the “Gibbs scheme”, made up of several such conditional sampling steps, it draws new samples from every subspace, so by the end of one full iteration, a new sample has been drawn for all free parameters. This is then repeated to draw as many samples of the full parameter space as required.
This structure allows us to sample the parameters of different components of the data model separately, conditioning on all the other components’ parameters in each sub-step of the Gibbs scheme. In this sense, Hydra is modular: the conditional sampling steps don’t need to know anything about one another except for what the most recent state of the data model was from the previous step. This makes it relatively straightforward to add new data model components and sampling steps as long as they handle the necessary inputs (the current state of the data model) and outputs (generally the updated data model, or a component thereof) in a standardised way.
For brevity, each conditional sampling step of the Gibbs scheme is referred to as one of the “heads” of Hydra (a reference to the many heads of the code’s mythological namesake).
We now summarise some of the currently available heads of Hydra.
Linearised gains
The per-antenna complex gains are modelled as a function of frequency and local sidereal time (LST). The gain model has a fixed prefactor (the ‘fiducial’ gain model for each antenna) times a small perturbation that can be sampled, i.e.
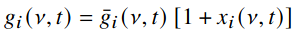
The perturbation is constructed from a discrete set of 2D Fourier modes (i.e. modes in delay and fringe-rate, the Fourier duals of frequency and LST), which needs not be complete or orthonormal.
Gains always appear quadratically in the data model, i.e. all visibility data points involve the product of two antenna gains. We do not know of an efficient way to sample directly from the conditional distribution of a large number of parameters that are quadratic however. At best, we could condition on the parameters for all but one antenna, which would result in a multivariate Gaussian conditional distribution for the parameters of that antenna. We could then iterate through all antennas. This is onerous for large antenna arrays with potentially hundreds of antennas, and risks seriously increasing the correlation length of the Monte Carlo chain, as it would take a long time to explore correlated directions in the joint antenna gain parameter space
Instead, we make an approximation: that the gain perturbations are sufficiently small that the quadratic term of the antenna gain product can be neglected, i.e. in the data model, we keep only terms that are linear in the antenna gains:
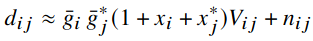
As long as this approximation is valid, we have a data model that is linear in all the gain parameters, and so we can write down a joint conditional distribution for all the gain parameters that is a multivariate Gaussian. Multivariate Gaussians can be sampled from directly bu solving a linear system (which looks like the Wiener filter plus some random fluctuation terms).
We do not assume redundancy of the array in our gain model. Nor do we apply a smoothing or similar; a smooth gain model is naturally obtained by including only Fourier modes with low delay/fringe rate values. Since arbitrarily complicated structure can be included in the fiducial gain model, which is fixed for each antenna, particular features of the gains at higher Fourier wavenumbers can be included in there if necessary, without greatly increasing the number of parameters. Care must be taken to understand how the small perturbations will modulate the structure of the fiducial gain model however (e.g. structure can appear at beat frequencies).
Point source amplitudes
We model discrete point sources as actual point sources, i.e. there is no pixelisation or gridding. The complex visibility of each source is calculated directly. The frequency spectra are taken from an input catalogue, where they will normally have a power-law form, but can take on other spectral shapes too. Each source can have a different frequency spectrum, but this spectrum is fixed, i.e. there is no source frequency spectrum sampling step at the moment.
The catalogue amplitude is taken as a fixed fiducial amplitude for each source, and we draw samples of fractional perturbations to this. These perturbations can be arbitrarily large; there is no linearisation assumption here.
Because the data model is linear in the source amplitudes (after conditioning on everything else), we can draw samples of the amplitude fractional perturbations directly from a joint multivariate Gaussian distribution for all of the sources.
Discrete regions of diffuse maps
To model diffuse emission, we take input Healpix maps as a function of frequency, e.g. from the Global Sky Model. Each pixel is modelled as a single point source, with an amplitude corrected by the pixel area, but no other attempt to take into account the extended nature of the pixels. The pixel’s frequency spectrum is taken from the input sky model, and is currently fixed.
This point source approximation will become poor for low map resolution (i.e. when the Healpix nside parameter is small), and when the pixel size is comparable to or larger than the baseline angular scale. Another issue is when the pixels set below the horizon; because only the pixel centre is tracked, there will be a “step” in the visibility model when the pixel centre sets, rather than a more gradual decrease in its contribution to the visibility model as progressively more of the pixel goes below the horizon. If the primary beam response is low enough near the horizon, this effect will be mitigated however.
The sky model is then decomposed into a set of discrete “regions” by calculating a crude estimate of the power-law spectral index for the frequency spectrum in each pixel. Pixels with similar spectral indices are grouped together within the same region, regardless of their location on the sky. The total visibility response of each region is then calculated by summing over the visibilities for all its constituent pixels. This is taken to be the fiducial contribution to the observed visibility from each region, which we then perturb, in much the same way as we perturbed the amplitudes of the point sources (see above). Amplitude perturbation samples can then be drawn from a joint multivariate Gaussian distribution for all the regions, again as was done for the point sources.
Because the treatment of the region and point source models is so similar, the Hydra sampler bundles them together into a single joint sampling step. This is achieved by concatenating the linear operators that project from source/region amplitude parameters to visibility model. These operators are then used to construct the matrix operator for the large linear system (the “Gaussian constrained realisation” equation) that can be solved to yield samples drawn directly from the joint point source + diffuse region conditional distribution.
Note that, while the spectral dependences are fixed, the pixels within each region are not forced to have exactly the same spectral index, and so some spatial structure in the frequency dependence is preserved. Because the visibility response from each region is constructed from many individual pixels, as a region sets below the horizon, its contribution will gradually tail off as its constituent pixels set, up to the pixel = point source approximation described above.
The process of splitting the diffuse model into regions according to spectral index is somewhat arbitrary, and other splitting methods could easily be included. For the current method, settings are provided to do some smoothing of the spectral index map before dividing it into regions to allow smoother region edges and to yield regions with more contiguous pixels. The number of regions to use can also be chosen.
Spherical harmonic modes
Another way of modelling diffuse emission is to specify a set of spherical harmonics which define a temperature map at some reference frequency. In the current model, this map is then multiplied by a global power law, common to all pixels/spherical harmonic modes. The spherical harmonic modes themselves are complex, but because they are assumed to derive from a real-valued temperature map, negative $m$ modes and the imaginary parts of $m=0$ modes are redundant and are not included in the set of free parameters.
Only the modes up to a chosen maximum $\ell$ value are included in the model. Care must be taken to match the resolution of the model with the available baseline lengths etc. The number of modes scales like $(\ell_{\rm max} + 1)^2$, so for large maximum $\ell$ values, the number of free parameters can become quite large.
The visibility response function for the spherical harmonic modes is again calculated using a point source approximation for a set of Healpix pixels. For each spherical harmonic mode (real and imaginary parts), a Healpix map is generated at some chosen nside. The response is then simulated by summing the visibilities from each pixel (which has been approximated as a point source) over the whole map. See the above section on diffuse map regions for caveats regarding this approximation.
Spherical harmonic angular power spectrum
For a spherical harmonic component model that has factorisable spatial and spectral parts (i.e. there is an angular map times a global frequency dependence), we can also sample the angular power spectrum of the spherical harmonic modes, $C_\ell$. This angular power spectrum acts as a prior in the spherical harmonic mode conditional distribution discussed above. Turning this around, the conditional distribution for the angular power spectrum depends only on the current set of $a_{\ell m}$ values, i.e. it can be written as $p(C_\ell | \{a_{\ell m}\})$, and does not directly depend on the data or the other model components.
With a uniform prior on $C_\ell$ itself, the conditional distribution has the form of a product of independent inverse Gamma distributions for each $\ell$ value, and so we can simply draw an appropriately-scaled inverse Gamma random variate for each $C_\ell$. The scaling depends on the “empirical” power spectrum, which is just the sum of the squares of the spherical harmonic modes, $\sigma_\ell = \sum_{m} |a_{\ell m}|^2$.